| Zöözi kanttori |
| Petri Keckman <keckman@mbnet.fi> |
| Edellisessä Sakussa artikkelissani "Suhtari" romutin nykyfysiikkaa. Tässä Sakussa romutan matematiikan perusteita. Painotan, että artikkelini täyttävät tieteellisen ja loogisen pätevyyden, vaikka niissä on osittain pieni humoristinen perusvire - matematiikkakin voi olla hauskaa! Jos nykypäivän tieteilijät eivät artikkeleitani noteeraa, niin sen kyllä tulevat tekemään tulevaisuuden tieteilijät. Tässä artikkelissa perustelen väitteitä, että R=Q ja että numeroituvuuden käsite on ristiriitainen. Ai mikä se on?
Aloitetaan alusta: Sir Georg Numeroituvuus merkitsee sitä, että joukon X kaikki alkiot voidaan luetella jossakin järjestyksessä siten, että niihin jokaiseen liitetään eri järjestysnumero 0,1,2,... Voisi äkkiä ajatella, että esimerkiksi murtolukujen joukko olisi "mahtavampi" kuin luonnollisten lukujen joukko, sillä voidaanhan kaikki luonnolliset luvut kuvata minkä tahansa kahden erisuuren murtoluvun a ja b väliin vaikkapa kuvauksella f(n)=b-(b-a)/(n+1). Josta siis f(0)=a ja f(n) lähestyy b:tä kun n lähestyy ääretöntä. f(0)=b-(b-a)/(0+1)=b-b+a=a ja f(99999999)=b+(b-a)/100000000. Esimerkiksi jos a=1,2 ja b=1,3 saadaan:
Seuraavassa kuvassa on vielä esimerkin vuoksi tarkasteltu tilannetta kun a=18,3 ja b=18,8. Keskellä on kokonaislukuakseli, josta numerot 0..27 on kuvattu välille a..b. Alla on lueteltu lisää lukuja.
a ja b voidaan valita siis mielivaltaisen läheltä toisiaan, ja tällaisia välejä mahtuu mihin tahansa kahden annetun luvun väliin vielä äärettömän monta, ja vaikka niiden pituus lukuakselilla voidaan saada mielivaltaisen lähelle nollaa, niin näihin kaikkiin väleihin erikseen voidaan kaikki luvut 0,1,2,... kuvata. Jokaisessa välissä "riittäisi siis lueteltavaa kaikille luonnollisille luvuille loppuelämäksi". Tuntuu oudolta, että kuitenkin on olemassa määritelmä "yhtä mahtavuus", joka siis sanoo, että luonnollisten lukujen joukko N on yhtä mahtava kuin koko murtolukujen joukko Q, kun näyttäisi ilmeiseltä, että murtolukujen joukko Q on äärettömän monta kertaa "suurempi" kuin N. Joukkojen Q ja N "yhtämahtavuutta" perustellaan eräänlaisella luettelotempulla. Kaikki rationaaliluvut eli murtoluvut ovat siis määriteltävissä kahden luonnollisen luvun n ja m jakolaskuna eli osamääränä n/m. Q on niiden alkioiden n/m joukko, missä n ja m kuuluvat N:ään. Tehdään kaksiulotteinen taulukko, jossa riveittäin kasvaa n ja sarakkeittain m.
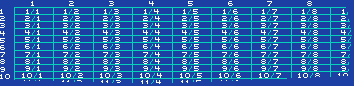
Annetaan nyt jokaiselle murtoluvulle järjestysnumero siten, että luvut luetellaan vinottain:
Jokaiseen annettuun murtolukuun n/m voidaan näin liittää yksi ja määrätty luonnollinen luku. Sivuutan tässä nyt negatiiviset luvut, sillä ne voidaan lisätä luetteloon muodostamalla toinen samanlainen taulukko ja ottamalla joka toisen luvun sieltä. Murtolukujen joukossa samaistetaan luvut, jotka ovat muotoa (i*n)/(i*m) ja n/m. Esimerkiksi kaikki vinoakselilla n,n olevat luvut 1/1, 2/2, ... ovat samat kuin 1, joista vain ensimmäinen 1/1 otetaan ja muut pyyhitään yli. Samoin 6/2 = 3/1 jne... Näihin jokaiseen on kuitenkin liitetty luonnollinen luku. Luonnollisia lukuja pitäisi olla siis "niin paljon enemmän", että niitä on varaa tuhlata ylimääräisten numerointiin, vaikka edellä vähän jo perustelin, miksi niitä on äärettömän monta kertaa vähemmän. Vaikka murtoluvut voidaan Cantorin ja nykymatemaatikoiden mielestä luetella, niin reaalilukuja - joihin kuuluvat myös päättymättömät desimaalikehitelmät kuten 0,1234567891011121314..., pii=3,141592643589 jne. ei sentään voida. Heidän todistuksensa on seuraavanlainen (perustuu vastaväitteeseen): oletetaan, että kaikki reaaliluvut väliltä 0...1 (edes tältä väliltä) voitaisiin luetella jossakin järjestyksessä, esimerkiksi: I:
Konstruoidaan nyt luku r siten, että käydään listaa läpi ja jokaisen luvun r(n) kohdalla lisätään r:ään luvun r(n) n:s desimaali siten, että siihen lisätään 1. Jos luvun r(n) n:s desimaalinumero on 3, laitetaan r:ään 4. 9:stä laitetaan 0. Luvun r alku näyttää siis: 0,9887... r(0)=0.89737
|
8+1=_9_
r(1)=0.57677
|
7+1=_8_
r(2)=0.56780
|
7+1=_8_
r(3)=0.45466
|
6+1=_7_
Luku r tulee siis eroamaan kaikista luetelluista luvuista, koska se eroaa niistä jokaisesta ainakin yhdellä desimaalilla. Koskaan ei tiedetä, voisiko luvun r(n) kohdalla konstruoitu luku r olla kuitenkin jo seuraava, mutta seuraavan luvun kohdalla jatketaan luvun r konstruointia siten, että se eroaa kaikista jo luetelluista luvuista. Kuinka tämä eroaisi siitä, että todistettaisiin, ettei edes luonnollisia lukuja voida luetella missään järjestyksessä vastaavalla tavalla? Oletetaan, että luonnolliset luvut voitaisiin luetella jossakin järjestyksessä. f(0)=0 Yleensähän luonnolliset luvut luetellaan suuruusjärjestyksessä 0,1,2,... mutta tässä nyt oletetaan, että ne olisi voitu edes jossakin järjestyksessä luetella. Konstruoidaan nyt luku i siten, että aina luvun f(n) kohdalla siihen lisätään f(n)+1. Aluksi i on siis 0 ja siihen lisätään f(0):n kohdalla f(0)+1. Saadaan
Luku i eroaa varmasti kaikista jo luetelluista luvuista, onhan se niitä kaikkia suurempi. Siis luonnollisia lukuja ei voida luetella? Samoin kuin ei reaalilukuja. Vai miten tämä eroaa todistuksesta, jossa todistettiin että reaalilukuja ei voida luetella? Jos yrität selittää jotain, että reaalilukuja koskevassa todistuksessa ollaan jo etukäteen varmoja, että konstruoitua lukua ei tule olemaan luettelossa, kun taas esimerkiksi lueteltaessa luonnollisia lukuja ihan tavallisessa suuruusjärjestyksessä, ollaan varmoja, että mille tahansa luvulle n löytyy siitä paikka - se on nimittäin n:ntenä luettelossa - niin se ei päde. Sillä voidaanhan reaalilukuja yrittää luetella toisella tavalla: aina luvun r(n) kohdalla konstruoitu luku r siirretään seuraavaksi ja sitä seuraavia yhden pykälän eteenpäin. Siis edellisen yrityksen I tapa luetella reaalilukuja muutetaan seuraavanlaiseksi: II:
Tässä luettelossa on nyt tilanne jokaisen luvun kohdalla sellainen, että vaikka kuinka yritetään konstruoida desimaalilukua, jota ei voida luetella, niin se änkeää itsensä heti seuraavaksi. Ihan sama kuin jos luonnollisia lukuja lueteltaessa konstruoitaisiin jokaisen luvun kohdalla n luku n+1 ja todistetaan, ettei luonnollisia lukuja voida luetella, koska jokaisen luvun kohdalla on konstruoitavissa luku, joka ei ole esiintynyt listassa. Tällä asialla on nyt artikkelissani sellainen painoarvo, että jos matemaatikot eivät tähän reagoi ja vastaa, missä teen päättelyssäni virheen, niin samoin kuin katson edellisessä Sakussa kumonneeni suhteellisuusteorian, niin nyt katson kumonneeni matematiikan perusteet, ellei tähän vastata (koska ei voida vastata muuta kuin väärin perustein). Luonnollisia lukuja lueteltaessa ovat täsmälleen samat ehdot voimassa kuin tavassa yrittää luetella desimaalilukuja väliltä 0...1 todistettaessa ettei niin voi tehdä.
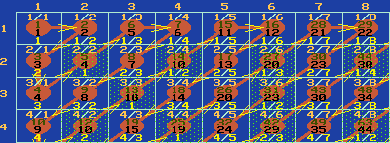
Mikä on se matemaattisen tarkasti ilmaistavissa oleva ero? Matemaatikoilta haluaisin kysyä tätä. Tosin matemaatikot eivät ikävä kyllä lue Sakua, kuten eivät ilmeisesti fyysikotkaan, sillä muutenhan he olisivat jo teilanneet edellisessä Sakussa olleen artikkelini? Matematiikanhan väitetään olevan tarkkaa ja eksaktia, eikä siinä saisi pitäytyä mihinkään "musta tuntuu" -todistuksiin. Kyllä minustakin tuntuu, ettei reaalilukuja voida luetella, mutta minusta tuntuu myös, ettei rationaalilukuja voida liittää yksikäsitteisesti luonnollisiin lukuihin. Ja itse asiassa minusta tuntuu, ettei edes luonnollisia lukuja voida luetella - tai ainakaan niitä ei voida luetella samasta syystä ja samanlaisen todistuksen perusteella kuin desimaalilukuja. Palataan rationaalilukujen luettelointiyritykseen taulukkotempulla, josta muuten voidaan todeta, että käsittääkseni mitään suoraa lauseketta ei ole olemassa murtoluvun liittämiseen luonnolliseen, vaan se täytyy aina algoritmillisesti konstruoida. Jos ei tarvitsisi pyyhkiä yli supistetussa muodossaan olevan luvun useita esiintymisiä, niin sitten lukuun n/m liitetty järjestysnumero i olisi helposti laskettavissa: i=(n-1)(n/2)+(n-1)(m-1)+m(m-1)/2. Tosin tämä lauseke pätee, jos lukuja luetellaan aina oikealta ylhäältä vasemmalle alaspäin eikä vuorotellen, mutta vastaavanlainen lauseke jossa esiintyisi tekijänä mod(2) saataisiin tässä käytetylle siksak-luetteloinnille. Mutta koska näin ei voida tehdä, ja eri murtolukujen samat supistetut esitysmuodot samaistetaan, ei ole olemassa lausekkeellista bijektiivistä kuvausta N->Q. Meillä on siis vain käytäntö ja äärelliset tietokoneet murtolukujen liittämiseen luonnollisiin lukuihin. Alla olevan kuvan soluissa alkioina olevat luvut ovat:
Mitä kauemmaksi luettelossa mennään, sitä suuremmaksi tulee ylipyyhittyjen murtolukujen määrä suhteessa kaikkiin osamääriin. Ensimmäinen ylipyyhitty on siis 2/2, joka on viides lueteltu luku. Miljoonannen luvun kohdalla ylipyyhittyjä on 39,1196 %.
Lukujen luettelointijärjestyksestä johtuu, että jos luku yleensäkään voidaan sieventää, sen sievennetty versio on jo lueteltu, sillä luku i/j esiintyy luettelossa aina ennen lukua n*i/n*j. Tämä ylipyyhittyjen määrän kasvu ei ole niin oleellista, mutta onpahan vain artikkelissa mukana, kun tietokoneella ja luvuilla leikkiminen on niin hauskaa. Mutta seuraava asia on (oleellinen): Kun tarkastellaan murtolukuun n/m liitettyä järjestyslukua (suoraa tai supistetut huomioiden) ja verrataan sitä suurimpaan taulukossa esiintyneeseen murtolukuun n/m listaamalla niitä alusta hieman...:
...havaitaan, että järjestysluku kasvaa huomattavan nopeasti ja on jokaisella vinorivillä suurempi kuin mikään sillä esiintyvä murtoluku, johon se on liitetty. Suurin murtoluku joka sijaitsee vinorivillä (ks. seuraava kuva alla), jolla sijaitsee luku n/m on ensimmäisellä sarakkeella sijaitseva (n+m-1), ja suurin suorista järjestysluvuista, jotka ylipäätänsä voidaan laskea, on (n+m-1)*(n+m)/2 ja näiden suhde 2/(n+m) lähestyy nollaa kun n+m kasvaa. Luonnollisten lukujen joukko on kuitenkin murtolukujen aito osajoukko ja kaikille luonnollisillekin luvuille löytyy järjestysnumero. Varmasti jokaisella luonnollisella luvulla n on paikkansa taulukossa, onhan se n/1 ja esiintyy siis n:n rivin ensimmäisessä sarakkeessa. Mutta tästä huolimatta jokaisen vinorivin kohdalla voidaan konstruoida n kappaletta lukuja - nimittäin kaikki järjestysluvut - jotka eivät ole esiintyneet vielä listassa. Siis järjestysluvuille ei ole vielä löytynyt järjestyslukua. Eikö tilanne muistuta taas samaa tapaa, jolla Cantor todisti, ettei reaalilukuja voida luetella? Varsinkin kun korostetaan sitä, ettei ole olemassa matemaattista lauseketta lukuun n/m liitetylle järjestysluvulle, koska ei tiedetä, kuinka monta sitä ennen on pyyhitty yli. Tai jos ylipyyhityt jätetään vain noteeraamatta eli luonnollisia lukuja "tuhlataan" ylimääräisten luettelointiin, niin sitten on lauseke (n-1)(n/2)+(n-1)(m-1)+m(m-1)/2, joka liittää murtolukuun n/m sen järjestysluvun.
Järjestysluku voidaan muuten päätellä pinta-aloja tarkastelemalla. Päätellään yllä olevasta kuvasta esim. ruudun 7/6 suora järjestysnumero. Koko eri väreillä väritetyn neliöosan pinta-ala on 12*12=(7+6-1)*(7+6-1). Siitä vähennetään alemman puolikkaan pinta-ala (12*11)/2 - joka voidaan päätellä siitä, että sarjan 1+2+...+n summa on (n+1)*(n/2) (Gaussin summa: ensimmäinen + viimeinen, toinen plus tokavika,.. niiden kaikkien arvo on n+1 ja niitä on n/2 kappaletta) - ja lisätään joko 7 tai 6 riippuen siitä, kumpaan suuntaan ollaan luettelemassa vinoriviä, jolla 7/6 sijaitsee. Ilmeisesti 7, koska (7+6) mod 2 = 1. Siis n/m:n suora järjestysnumeron on päätelty olevan (n+m-1)(n+m-1)-(n+m-2)(n+m-1)/2 johon lisätään joko n tai m riippuen siitä kumpaan suuntaan ollaan kuljettu eli lausekkeena esim.:((n+m) mod 2)(n+m)-m ja lauseke olisi muodossa (n+m-1)(n+m-1)-(n+m-2)(n+m-1)/2+n, jos vinorivejä kuljettaisiin aina samaan suuntaan, ja sieventyisi yllä antamaani muotoon. Mitä haluan tarkasteluillani sanoa? Väittääkö, että taulukosta puuttuu jokin murtoluku n/m? Ei, sitä en halua sanoa ainakaan jos minun pitäisi kertoa, mikä luku siitä puuttuu, mutta ei siitä seuraa, että numeroitavuuden käsite olisi järkevä tai että Cantorin todistukset olisivat sitä tai että koko äärettömän käsitteessä olisi mieltä. Jos N:ään kelpuutetaan kaikki luvut n+1 jos n kuuluu N:ään, niin samoin kaikki murtoluvut muotoa a+1/n kelpuutetaan Q:hun jos a kuuluu Q:hun. Tästä seuraisikin, että reaaliluvut kuuluisivat Q:hun, sillä ne on määritelty rationaalilukujen päättymättöminä sarjoina. Esim. pii voidaan esittää muodossa pii=1-1/3+1/5-1/7+..., joka kuuluisi murtolukuihin samoin kun kaikki luvut n+1 kuuluvat aina N:ään jos n kuuluu N:ään. Äärettömän käsitteeseen on matematiikassa törmätty raja-arvoja määrittelemällä. En tiedä, kuinka matemaatikot suhtautuvat esim. luvun 33333.../111111... raja-arvoon. Sehän on ilmiselvästi kolme. Tässä vain käytetään äärettömän pitkiä lukuja. Kuuluvatko ne N:ään? Jos eivät, niin millä perusteella? N:äänhän kuuluvat kaikki muotoa n+1 olevat luvut, jos n kuuluu N:ään. Ja luku 333333... voidaan määritellä äärettömänä summana 3+30+300+3000+... joka kuuluu N:ään, vaikka termejä olisi - ja kun niitä on - äärettömän monta. Tätä kautta N saataisiinkin yhtä mahtavaksi kuin R, jos luvuiksi kelpuutetaan äärettömän pitkät. Jos ei kelpuuteta, niin miksi muuten ylipäätänsä leikitään äärettömillä luvuilla, kun kaikki reaalinen on äärellistä (paitsi ehkä aika - paitsi ihmiselämälle)? Rationaalilukujen luettelotempusta totean vielä: Esitin jo taulukkoluetteloon liittyen funktion F(n,m), jolla liitettiin rationaalilukuun (n/m) sen luonnollinen "luetteloluku" i = (n+1)(n/2) + (n-1)(m-1) + m(m-1)/2. Löytyykö tälle selkeää käänteiskuvausta ts. kahta lauseketta f(i) ja g(i), joilla luonnollisesta luvusta i saataisiin selville sitä vastaava murtoluku f(i) / g(i) = n / m, ilman että se täytyy laskea tietokoneella? Totesin, että siinä tapauksessa, että ylipyyhityt luvut huomioidaan, sitä ei voida laskea suoraan vaan se täytyy algoritmillisesti tutkia. Sinänsähän se on yksikäsitteisesti määrätty. Mutta jos ylipyyhittyjä ei huomioida - tai siis ei poisteta ollenkaan, niin suora yhtälö järjestyslukua i vastaavalle murtoluvulle löytyy. Siis meillä ovat voimassa yhtälöt:
Toisaalta kuviota tarkastelemalla voidaan todeta: Josta m:lle toiseen asteen yhtälön ratk.: Siis: Tästä saadaan n:lle 4. asteen yhtälö, josta se voidaan ratkaista i:n suhteen ja sijoitetaan ratkaisu 1:een, josta ratkaistaan m i:n suhteen. Siis m/n on ratkaistavissa lausekkeellisesti järjestysluvusta i. Eli vaikka osittain saadaankin analyyttinen bijektio aikaiseksi myöskin N -> Q, (paitsi että tässä nyt taas jätetään huomioimatta se että Q:ssa luku n/m=(i*n)/(i*m) ja siis ylipyyhintää ei tehdä) mutta silti, yhtämahtavuuden määrittelyssä, tai koko äärettömyyden käsitteessä ei ole mieltä. Maalijoukko täytyy määritellä siten, että kaikkien niiden alkioiden, jotka ovat kuvattuja Q:sta N:ään, täytyy myös olla kuvauksen N -> Q lähtöjoukossa. Ja tämä on mahdotonta, sillä aina kun otetaan uusi N:n alkio käyttöön, niin sekin pitäisi pystyä kuvaamaan, mutta sille kuvausta etsittäessä joudutaan ottamaan yhä uudempia ja aina vain isompia N:n alkiota käyttöön. Äärettömyyttä täytyy tarkastella siten, että mitä tapahtuu maali- ja kuvajoukoille siinä tilanteessa kun niitä alkioita "luetellaan". Jos väitetään, että näin ei ole, niin sitten meidän täytyisi hyväksyä myös se, että Q on yhtä mahtava kuin R. Koska reaaliluvut ovat määriteltyjä rationaalilukujen päättymättöminä sarjojen summina. Jos tarkastellaan käsitettä kaikki reaaliluvut (johon siis kuuluvat rationaali- ja irrationaaliluvut) ja käsitettä koko rationaalilukujen joukko, niin täytyyhän tähän hyväksyä myös kaikki siihen kuuluvat vaikka äärettömän pitkätkin sarjat. Ja koska ne ovat sellaisiksi määriteltyjä (reaaliluvut), niin ne kuuluvat Q:hun. Koska jos luku a on rationaaliluku niin luku a+b on rationaaliluku. Yhtä hyvin kuin jos n on luonnollinen luku, niin n+1 on luonnollinen luku, aina. Yhtä hyvin kuin hyväksymme kuinka suuren luvun tahansa äärettömän suureen luonnollisten lukujen joukkoon N, niin meidän on hyväksyttävä äärettömän pitkät rationaalilukujen summat (a+b+...) joukkoon Q. siis Q = R. Artikkeliin kuuluvilla C-kielisellä oheisohjelmilla canttori1.exe ja canttori2.exe voidaan tuottaa artikkelissa käytettyjä kuvia. canttori2.exe:lle voidaan antaa parametriksi joko 1, 2 tai 3. Lisäksi pari muuta ohjelmaa, joilla listataan lukuja. Ohjelmat.lha (50 kt, C-kieliset lähdekoodilistaukset ja Amiga-exet) |
Cantor (1845-1918) loi välineistön ja käsitteet, joilla äärettömät joukot saatiin matematiikkaan. Äärettömien joukkojen teoriassa on käsite "numeroituvuus" tärkeä. Jokin joukko X on numeroituva, jos se on "yhtä mahtava" kuin luonnollisten lukujen joukko N={0,1,2,... .}. Yhtä mahtava se taas on, jos - ja vain jos - löytyy yksikäsitteinen kuvaus X:stä N:ään, jossa jokaiseen X:n alkioon voidaan liittää eri N:n alkio, siis luonnollinen luku, ja samoin jokaiseen N:n alkioon voidaan liittää yksikäsitteinen X:n alkio. Hienosti sanottuna kyseessä on bijektiivinen kuvaus.
[ Sekalaiset ] [ Sivukartta ]